In Water Vel Sensor
This section documented our journey to develop a low-cost water velocity sensor based on doppler effect!
Contents
20th November 2019
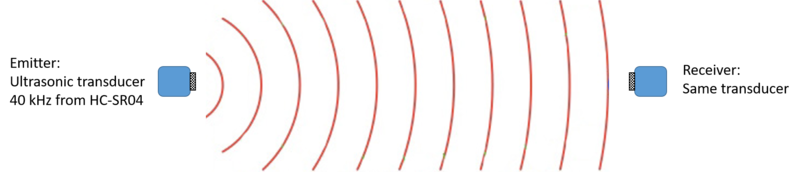
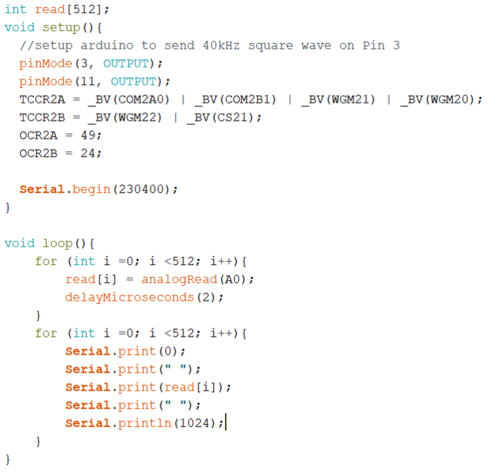
So the first task we are going to try is to use Arduino to generate 40 kHz square wave and emit that signal by using a ultrasonic transducer.
By facing another same transducer to the one emitting the ultrasonic signal, we can successfully detect that signal.
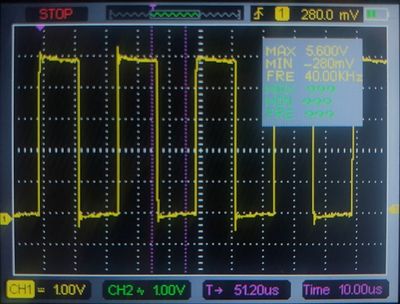
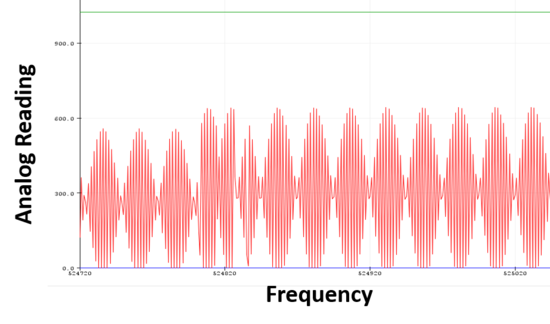
Figures below show the generated square wave from the emitting transducer (measured by an oscilloscope), and the detected wave signal from the receiver transducer (by using AnalogRead).
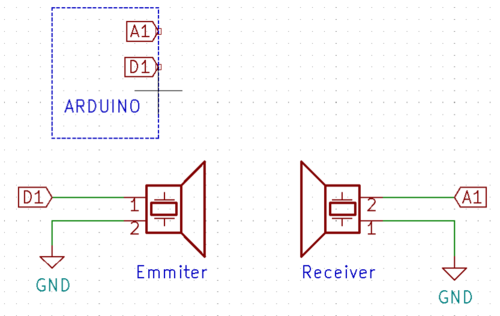
The figure here shows how we wire up the transducers with Arduino to conduct this quick test. The code we used is also attached here to show you how to use Arduino to generate a certain frequency.
21th November 2019
What are we going to try today is to place the two transducers next to each other and facing the same direction.
One emit the signal to a metal wall, and the receiver to detect the signal bounce back.
Multiple op-amps will be used to strength the signal to make it strong enough for Arduino to detect.
25th November 2019
For the arduino to effectively read the low amplitude high frequency signals it is going to need some assistance via external circuitry.
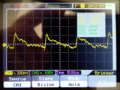
We tested an non-inverting op-amp design based on the LM324. This proved to have challenges reproducing the high frequency signals and after some diagnosis, we determined that the slew rate of the LM324 was too low.
The image above shows the limited slew rate experienced from the LM324N. In this domain the waveform appear as linear as the OpAmp attempts to match the proper signal. It demonstrated a slew rate of about 0.5 V / μS. To overcome this we will need to replace the LM324N with a better OpAmp.
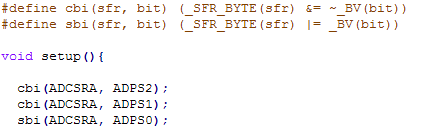
By default the Arduino ADC sample frequency is rather slow at 45 kHz. For our application we will need much faster sampling rates. Fortunately, the clock divider which the ADC runs on (default 32x) is user settable. In testing various values for this, a sample rate of 615 kHz was able to be achieved. <1>
This was accomplished via the following code:
26th November 2019
We tested out some LM883N and NE5532AP OpAmps to see if they performed better than the LM324 (they have a slew rating of ~5 V / μS so they should). Both worked much better than the LM324 being able to reproduce the waveform however, we found that the NE5532AP was better at higher gains.
It was found that the circuit below performed well at amplifying the AC signal of the receiver resonator.
The gain can be adjusted through resistors Ra and Rb via the formula: Gain = 1 + Ra/Rb
Issues were faced where very high noise was present on the output of the op-amp. Some investigation revealed that this was due to the same Arduino driving the 40 kHz squarewave as powering the op-amp. This limited the ability to receive low amplitude signals and made it difficult to detect the reflected ultrasonic waves. A temporary solution to this was to use separate Arduinos for the transmitted and receiver.
A noise profile was obtained by having the ultrasonic receiver covered and placed such that no ultrasonic frequencies would be measured by it. The op-amp output was then measured. Below are the measurements for the two-Arduino setup vs the one-Arduino setup.
The noise is improved in the two-Arduino setup however there is still a significant ammount, it may be necessary to make a PCB with better noise isolation for test which require higher sensitivity.
Arduino Sample Frequency
<1> From doing more test it appears that not all Arduinos are able to sample at the 615 kHz rate, a more reliable max appears to be 215 kHz.
Testing the values of the clock divider registers ADPS2, ADPS1, ADPS0, the following table was made indicating about the various sample frequency on a 16 MHz 5 V ATmega382P (Arduino Uno).
| ADPS2 | ADPS1 | ADPS0 | Sample Frequency (kHz) | Working |
|---|---|---|---|---|
| 0 | 0 | 0 | 325 | No |
| 0 | 0 | 1 | 325 | No |
| 0 | 1 | 0 | 215 | Yes |
| 0 | 1 | 1 | 125 | Yes |
| 1 | 0 | 0 | 66 | Yes |
| 1 | 0 | 1 | 35.6 | Yes |
| 1 | 1 | 0 | 17.6 | Yes |
| 1 | 1 | 1 | 8.9 | Yes |
Arduino Frequency Measurement
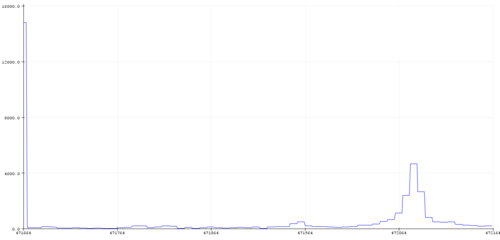
To measure frequency an DFT was performed on a 128 size sample at 215 kHz of the amplified ultrasonic receiver signal.The sample frequency was chosen as it was the highest stable, and the sample size as this was the limit of the ATmega382p's memory.
The y-axis height represents strength of that component frequency, and the x-axis the frequency bins, where eight bins corresponds to 1.7 kHz
Concerningly the peak height is at about 90 kHz, and the predominant frequency when measured with an oscilloscope is 40 kHz.
27th November 2019
Some thought was conducted into the feasibility of direct frequency measurement using the ATmega328p and extracting the Doppler shift digitally.
The velocity is given by the equation: v = c/2 (fd/f) cos(θ), where c is the speed of sound, fd is the Doppler shift, f is the emitted frequency, and θ is the angle between the flow and sensor.
Let us assume that the sensor is parallel to the flow (θ = 0). By Nyquist-Shannon sampling theory, to detect a frequency at f we need the ATmega328p to sample at 2f. Applying a DFT to this sample gives a frequency resolution Δf of 2f/N, where N is the number of samples. Therefore, making the substitutions fd = 2f/N, θ = 0, we get: Δv = c/2 (2f/(f*N)) = c/N
For water (c = 1500 m/s) and a velocity resolution of Δv = 0.1 m/s this implies that 15 000 samples would need to be taken. This would require an amount of memory well beyond the 2 kB of the Arduino (which can realistically only store 128 samples).
This implies that direct measurement of the Doppler shift is not feasible and that some signal pre-processing is necessary. The idea is to extract the Doppler shift so that we can have a easier time sampling the lower frequency Doppler shift signal.
There are two approaches which we are going to trial, amplitude demodulation, and a heterodyne converter.
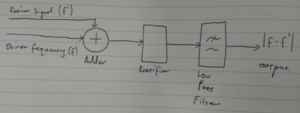
Amplitude Demodulation
The premise of the AM demodulator is that the sum of the two signals produces a beating frequency (f' - f) which is conveniently also the Doppler shift fd. The rectifier eliminates the negative peaks of the resultant sum, and the low pass filter blocks the high frequency carrier wave of the signal, leaving only the low frequency Doppler shift.
The draw back of this method is that the signal is very weak, and it is difficult to scale to higher frequencies.
A pathfinder version of this circuit was constructed as indicated in the diagram. The circuit performed well for high amplitude frequencies, as generated by a pair of Arduino Unos (5 Vpp ~40 kHz square wave). For one input at 40 kHz and the other at ~42 kHz an output was obtained of ~2 kHz or the difference between the two frequencies. The amplitude of this signal was about 500 mV.
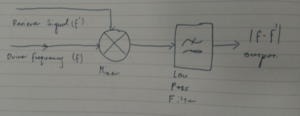
Heterodyne Pre-Processing
The Heterodyne is more standard for high frequency Doppler shift applications, the mixer multiplies the two signals. For two sine waves with frequencies fa and fb, their product will be the sum of cosines with frequencies |fa-fb| and |fa + fb|. For fa = f', and fb = f, the lower frequency signal is the Doppler frequency, which can then be isolated from the higher frequency using a low pass filter. This method provides the advantage of it being proven to work at a wide range of frequencies, in excess of 500 MHz.